I’m going to step up on my soapbox for the concept of appreciation being built into cap rates.  Can someone hand me a microphone… please?

Appreciation Explains Cap Rate Differences… Not!

It’s taught in Appraisal 101 that the difference in cap rates is appreciation.  Here’s a good quote I found to support that.

The cap rate only recognizes the cash flow a real estate investment produces and not the change in value of the property.

To get the unlevered rate of return on an investment the real estate investor adds (or subtracts) the price change percentage from the cap rate. For example, a property delivering an 8% capitalization, or cap rate, that increases in value by 2% delivers a 10% overall rate of return. The actual realised rate of return will depend on the amount of borrowed funds, or leverage, used to purchase the asset.

The above is worthy of becoming a new riddle for the Sphinx.  The first sentence says that the change in property value has nothing to do with the cap rate.  The second sentence says that the difference in two cap rates is appreciation (I suppose ceteris parabus applies – all other things being equal).  Well, if the cap rate has nothing to do with the change in the value of a property, then how could two cap rates that have nothing to do with the change in value be compared to produce a change in property value?  This is a job for The Riddler!

Now we move onto the last sentence, “the actual realized rate of return will depend on the amount of borrowed funds, or leverage, used to purchase the asset.”  And here I thought a computer bit could only be flipped two ways – on and off.  I suppose this is the neutral or null setting.  So what I take from this is that you can believe what you want – that appreciation is a part of cap rates or not, but your opinion doesn’t matter because the rate of return is based on leverage (or in other words, your financing terms).  Maybe this is all politics.  I’d say the Republican, Democratic and Independent constituencies have been very well served!

Beware Pandora’s Box

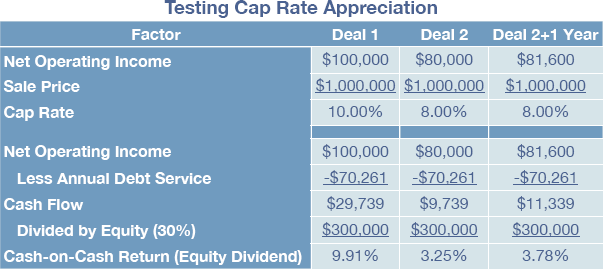
I just have to put the appreciation thing to the test.  Let’s use the example above provided to us by Wikipedia.  To this, let’s add a mortgage based on a 20-year amortization, an 8 percent interest rate and a 30 percent down payment requirement (a 70 percent loan-to-value ratio).

As you can see, t

The cash-on-cash return is over three times greater for the 10 percent cap rate deal given the same purchase price and loan terms.  ‘Makes sense – everything else being equal:  less net operating income means a lower cash-on-cash return.  Yes, but did you notice that the 8 percent cap rate only returns 3.25 percent, not 8 percent?

What’s the Diff?

So the quote above says the 2 percent difference in the 8 percent and 10 percent cap rates is appreciation.  This poses a problem and a question.  At what point is the 2 percent appreciation realized?  Certainly not on the day the property is bought, which is what is implied by using cap rates.  Let’s look at the third column labeled “Deal 2 + 1 Year”.  Here I’ve increased net operating income by two percent and this increases value by 2 percent.  The 8 percent cap rate stays the same yet the property has appreciated 2 percent.

So are the two the same?  The 2 percent appreciation translates into a $20,000 gain ($1,020,000 – $1,000,000).  Divide that by the $300,000 equity and you get a 6.67 percent return.  Nice.  Add to that the 3.25 percent cash-on-cash return from the cash flow and you have 9.91 percent – the same cash-on-cash return as that shown in the 10 percent cap rate deal!  We’ve done a mathematical proof that, indeed, the difference in the two cap rates is appreciation.

Well, we’re not done yet.  There is a difference.  The 10 percent return is realized at the end of year one when the 8 percent cap rate deal is sold.  Only then is the cash-on-cash return the same as it is on day one of the 10 percent cap rate deal.  Did you notice the one year difference there?  For lack of a better term, I’ll call that the appreciation time period.

So let me ask you this:  would you rather have a dollar today or dollar one year from now?  Sounds silly, I know, but it’s the foundation of discounted cash flow theory.  That dollar one year from now is worth less today than the dollar now.  I don’t want to get too mathematical but I just want to leave this thought with you:  if you discounted that return at the end of year one to the beginning of year one, would it be a lower return?  Shake your head up and down to simulate “yes”.

Still, there’s one more problem here.  If Deal 2, the 8 percent cap rate, went up by 2 percent, do you think that Deal 1, the 10 percent cap rate, stayed stagnant?  It would be more logical to consider that it also appreciated by 2 percent rather than think it stayed the same.  So what would that return be?  All the numbers we need are here.  The $20,000 appreciation translates into a 6.67 percent return for the appreciation factor.  Add that to the 9.91 percent cash-on-cash return the first year and we have a total return of 16.58 percent.  That’s a difference of… you guessed it… 6.67 percent, the appreciation factor.

And there you have the paradox.  You can’t appreciate the 8 percent cap rate deal by 2 percent and expect it to return the same total return on investment as the 10 percent cap rate deal because the 10 percent cap deal will appreciate by 2 percent too! The 10 percent cap rate deal will never equal the 8 percent cap rate deal unless it mysteriously stops appreciating.  Yet aren’t the two equated by saying an 8 percent cap + 2 percent for appreciation = a 10 percent cap?

Forget Me Nots

To keep the example simple, I’ve left out a few realities.  If you sell Deal 2 in a year, you’ve got closing costs.  The seller pays the state excise cost (generally up to 2 percent… oops, there goes your 2 percent appreciation!), the cost of an attorney and a few other piddly expenses.  Perhaps the property has to be sold through a real estate broker… now paying a 6 or 7 percent agent fee wipes out your positive return on investment, especially when combined with the state excise cost.  Now you know why people hold real estate for many years unless the market is so incredibly hot that appreciation greatly covers these expenses.  Classroom theory is fine, but it looks like it’s hit the brick wall of reality at full speed.

Let the Games Begin!

This is all just a warm-up for me.  In Part 3 I’ll really crack the whip and debunk why cap rates should not be used as an indication of your return.